
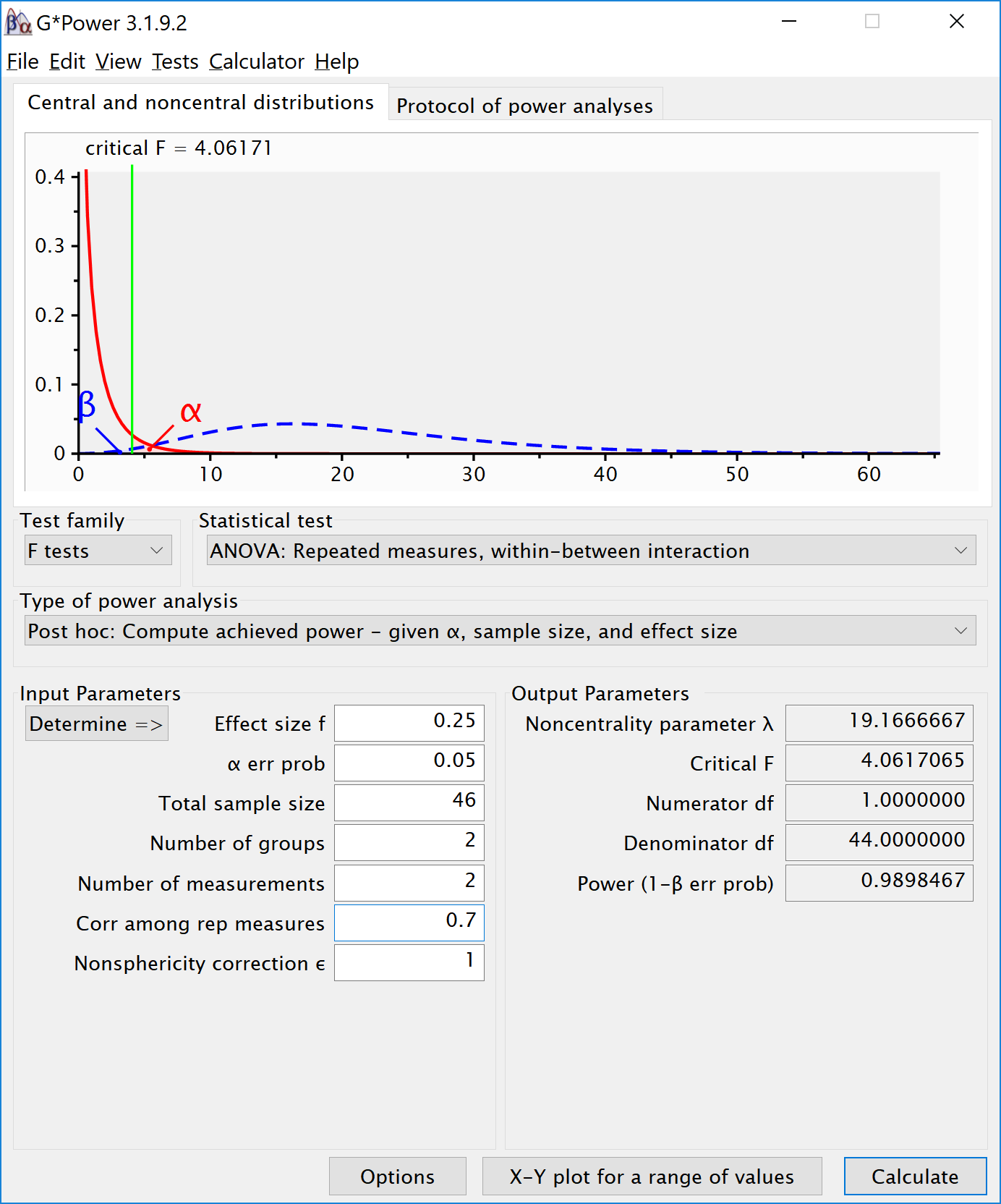
For this example the value will change to interaction.eta2 = 0.079. Since there is only one interaction in a 2-way ANOVA, this would be the quicker way to change the interaction effect size. The alternative way is to change the default value of interaction.eta2 = "small" when calling the n.multiway function.
Assigning the value for the estimated effect size follows the same set of conditions as the main effect’s effect size. The name of the interaction must be comprised of the names given to the treatments when the main effects were defined. This interaction effect can be assigned any value similar to the main effect names for this example it will be called int.eff1. The first way is to define the interaction the same way we defined the main effects and change its effect size from “small” to some other value. The default setting for interactions is set “small”, but this can be changed in two different ways. Main.eff <- list( name = "A", levels = 3)įor this example, the effect size of the interaction is known. # Example of using the default eta.sq setting There is a default setting of “small” for this value. Note: If the effect size for a main effect is going to be “small” then the value of eta.sq does not need to be included when creating the list for the main effect. Acceptable string values and their numeric equivalents are: “small” (0.01), “med” (0.06), and “large” (0.14). This can be either a numeric value greater than 0 or a character string. eta.sq - Estimated effect size for the treatment effect.This is always an integer that is 2 or greater. levels - The number of levels/groups in the treatment.This may be either a character string of the treatment name, an abbreviation, or a single character such as “A”. name - The name of the treatment effect.Main.eff2 <- list( name = "C", levels = 4, eta.sq = 0.215)Įach main effect is defined as a list and takes in three different values: The main effects may be assigned any variable name but for this example they will be called main.eff1 and main.eff2. Before the sample size calculations are made, the main effects must be defined. All of the effect sizes taken from the exercise were converted from Cohen’s f to eta-squared in order to input the numeric equivalent into the calculations. This study is investigating the effects of age ( A) and contingency of reinforcement ( C) on learning. This example study is a 2x4 ANOVA and is taken from exercise 8.15, p.400 of Cohen (1988).


 0 kommentar(er)
0 kommentar(er)
